TEKNİK ANALİZDE FİBONACCİ DÜZELTME SEVİYELERİ
Bir önceki yazımızda teknik analiz yöntemlerinden bahsetmiş ve önemli indikatörlerden biri olan Bollinger Bantlarına dair bazı temel bilgilere yer vermiştik. İstiyoruz ki; pay piyasasına olan ilgi tarihinin en yüksek yatırımcı sayısına ulaşarak farklı bir boyut kazanmışken değerli okurlarımıza bu konuda elimizden geldiği kadar faydalı bilgiler aktaralım. Bu sebeple teknik analiz yöntemlerinin içerisinde en önemli ve en popüler yöntemlerden bir diğeri Fibonacci Dizisini ve düzeltme seviyelerini finansal piyasalarda varlıklar üzerinde nasıl kullanıyoruz ve nasıl yorumluyoruz biraz açıklayalım.
Orta çağın en yetenekli matematikçisi olarak kabul edilen İtalyan bilim adamı Leonardo Fibonacci. Onu bu kadar bilinir kılan en fazla Hint-Arap Sayılarını Avrupa’ya getirmesi ile 13.yy başlarında yayımlanan Liber Abaci hesaplama yöntemleri kitabı ve bu kitapta bir örnek olarak yer alan modern sayılarla hesaplanmış kendi adıyla anılan Fibonacci Dizisinin yaratıcısı olmasıdır.
Altın Oran nedir?
Fibonacci oranları ile ilgili genel kuramlar basit bir sayı dizesini temel almaktadır. Fibonacci ilgili kitabında bunu kapalı bir ortamda tavşanların üremesiyle ilgili bir problemden yola çıkarak izah eder. Bu sayı dizesinde her rakam kendisinden önce gelen iki rakamın toplamına eşittir. Şöyle ki;
0, 1, 1(1+0), 2(1+1), 3(2+1), 5(3+2), 8(5+3), 13(8+5), 21(13+8), 34(21+13) ….
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …. şeklinde uzayıp giden ve genellikle “Fibonacci sayıları” şeklinde adlandırılan bu sayı dizisinin en önemli özelliği her sayının kendisinden bir önceki sayıya bölünmesi ile her aşamada gittikçe 1,618 rakamına yaklaşılmasıdır. Bugün sayı dizisindeki bazı sayıların bölünmesi ya da çarpılmasıyla bizi o altın orana götüren ve her yolun bizi belirli bir seviyeye götürdüğünü anlatan Altın Oran’ın ondalık gösterimi ise 1,618033988749894….şeklinde devam eder.
Bu oranlar içerisinde hem geri çekilme hem de sürdürme seviyeleri belirlenmiştir;
Fibonacci geri çekilme seviyeleri: 0.236, 0.382, 0.500, 0.618, 0.764
Fibonacci sürdürme seviyeleri: 0.382, 0.618, 1.000, 1.382, 1.618
Farklı özellikleri olan sayı dizisinin bir başka özelliği ise dizideki her üçüncü sayının 2’ye, her dördüncü sayının 5’e ve her altıncı sayının ise 8’e bölünebildiğidir. Özellikle sayı dizisindeki herhangi bir sayının 1,618 yani altın oran ile çarpımı bir sonraki sayıyı yaklaşık olarak vermektedir. Sayılar büyüdükçe altın orana yaklaşma oranı da artmaktadır. Dizideki herhangi bir sayının 0,618 katı ise bir önceki sayıyı yaklaşık olarak vermektedir. Yine sayı büyüdükçe yaklaşma oranı artmaktadır.
Örneğin;
Dizideki 34 sayısının 1,618 katı bizi 55.012’ye götürür. Dizideki daha küçük 5 rakamının ise 1.618 katı 8.09’a eşittir. Burada 34 sayısından bir sonraki 55 sayısına olan uzaklığın daha az olduğu görülür. Diğer özelliğe bakacak olursak da, 13 sayısının 0,618 katı bizi 8,034’e götürürken 89 sayısının 0,618 katının 55,002’ye gittiğini ve sayı büyüdükçe bir önceki sayıdan sapmanın azaldığını görebiliriz.
Diğer özellikleri arasında ise; dizideki herhangi bir sayının 2,618 katı iki sonraki sayıyı verirken, herhangi bir sayının 0,382 katı iki önceki sayıyı vermektedir. Dizide yer alan 1 ve 2 dışındaki tüm sayıların dört katının başka bir Fibonacci sayısı ile toplamı ise bir başka Fibonacci sayısına eşit olacaktır.
Peki, Finansal Piyasalarda Fibonacci Düzeltme Seviyeleri bir finansal varlık üzerinde nasıl kullanılır?
Fibonacci dizisi finansal piyasalarda bir varlığın alabileceği değeri tahmin etmek için kullanılır. Finans sektöründe bir varlığın hareketinin kesintisiz oluşması beklenmez. İşte Fibonacci Dizisi bu trendi belirlememizde yardımcı olabilecek analizler sunmaktadır. Teknik analizde Fibonacci oranlarından farklı şekillerde yararlanılması ile birlikte özellikle düzeltme seviyeleri en çok tercih edilen oranlar olması sebebiyle detaylarını inceleyeceğiz.
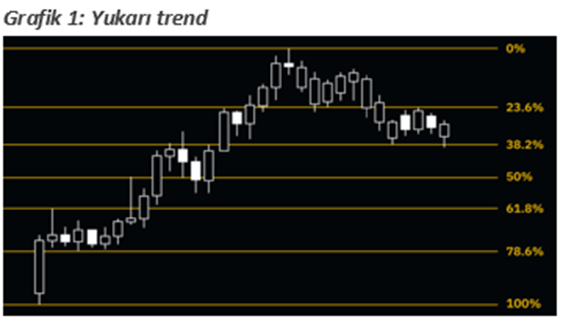
Bu analiz yönteminde trendin dip noktasından zirve noktasına çekilen çizgi yardımıyla dönüşlerin ya da düşüşlerin Fibonacci destek ve direnç seviyeleri elde edilir. Tek başına al sat sinyali ya da fikir vermek konusunda yeterli olmayabilir fakat diğer bazı teknik analiz seviyeleri ile çakıştığında orta-uzun vadeli destek ve direnç tespitinde oldukça başarılı olduğunu söyleyebiliriz. Birçok üründe yalnızca borsalarda değil emtia tarafı ve para birimleri içerisinde de kullanılabilen bir orandır. Kısa vade için de bu yöntem kullanılabilir ancak başarı oranı orta ve uzun vadeye göre daha düşüktür. Yani çok sık fiyat ve zaman aralıklarında değil de geniş aralıklarda daha tutarlı ve faydalı analizler verdiğini söyleyebiliriz. Temel mantık trendlerde dip ve zirve seviyeler arasındaki farkın her Fibonacci katsayısı ile çarpımının ayrı bir düzeltme seviyesini başarılı bir şekilde tespit etmesidir. Genellikle; 0.236, 0.382, 0.500, 0.618 katsayıları kullanılır ve bu katsayılar sayesinde bir analiz elde edilmek isteniyor.
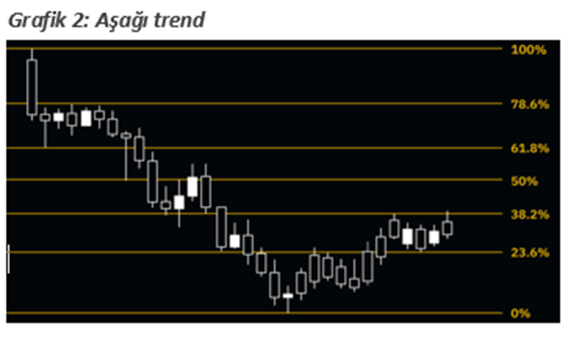
Fibonacci Düzeltmesini bir grafik üzerinde kullanmak istediğinizde, yükseliş trendinde (Bkz. Grafik 1) dip nokta 1 (ya da %100) ve tepe noktası 0 (%0) olur. Yükseliş trendinin üzerine çizilen Fibo düzeltmesi seviyesi, piyasanın geri çekilmeye başlaması durumunda test edilecek potansiyel destek seviyeleri hakkında bilgi verir. Bu durumun tam tersinde ise yani bir aşağı trend sırasında ( Bkz. Grafik 2) dip nokta 0 (%0) ve tepe nokta 1 (%100) olur. Fiyat aşağı trendde olduğu için bu durumda geri çekilmenin dip noktadan olduğuna yani bir sıçrama yaşandığına dikkat edilmelidir. Burada ise Fibonacci düzeltmesi aracı piyasanın yukarıya hareket etmesi durumunda potansiyel direnç seviyeleri hakkında bilgi verir.